Estimator Calibration

This is an exercise created to improve estimators’ ability to produce 90% Confidence Intervals that, in turn, contain the actual value 90% of the time. It was designed by Douglas Hubbard and explained in his book, “How To Measure Anything: Finding the Value of Intangibles in Business.”

Like the challenge of calibrating an instrument for measurements, this approach treats humans as the “instrument” and the estimates as a “measurement” that needs calibration. This need stems from the fact that - most of the time - estimators will either be overconfident or underconfident in their estimates. When estimators better understand their biases like this, they are better “calibrated” and better able to deliver 90% Confidence Intervals that stand the test of time.

A 90% Confidence Interval is an estimate that provides an upper bound and lower bound to a range of values that should - in the estimator’s opinion - contain the actual value, 90% of the time. If I’m asked to provide a 90% confidence interval for the temperature (in degrees Fahrenheit) tomorrow at noon, I might offer an upper bound of 85 degrees and a lower bound of 78 degrees (if I haven’t just checked the official forecast). Given what I know, I’m saying that in 9 out of 10 “possible futures”, I’m confident that the actual value should fall in that range.

The estimate is usually a forecast of a future value, but can also capture a “best guess” at a current value. As Hubbard explains, “The values should be a reflection of your uncertainty about the quantity” and “assessing uncertainty is a general skill that can be taught with a measurable improvement.” 

This improvement begins with a training activity to grow self-awareness. Individual estimators are asked to participate in a benchmark activity: They are asked 20 general knowledge questions, for most of which, they are not expected to know the exact answer. But Hubbard reminds us that, “the lack of having an exact number is not the same as knowing nothing.” For each question, the participant will be asked for a 90% confidence interval (not their guess at the answer). 

Here is an example of a 20 question calibration survey, from the appendix of “How To Measure Anything”:

‍

‍

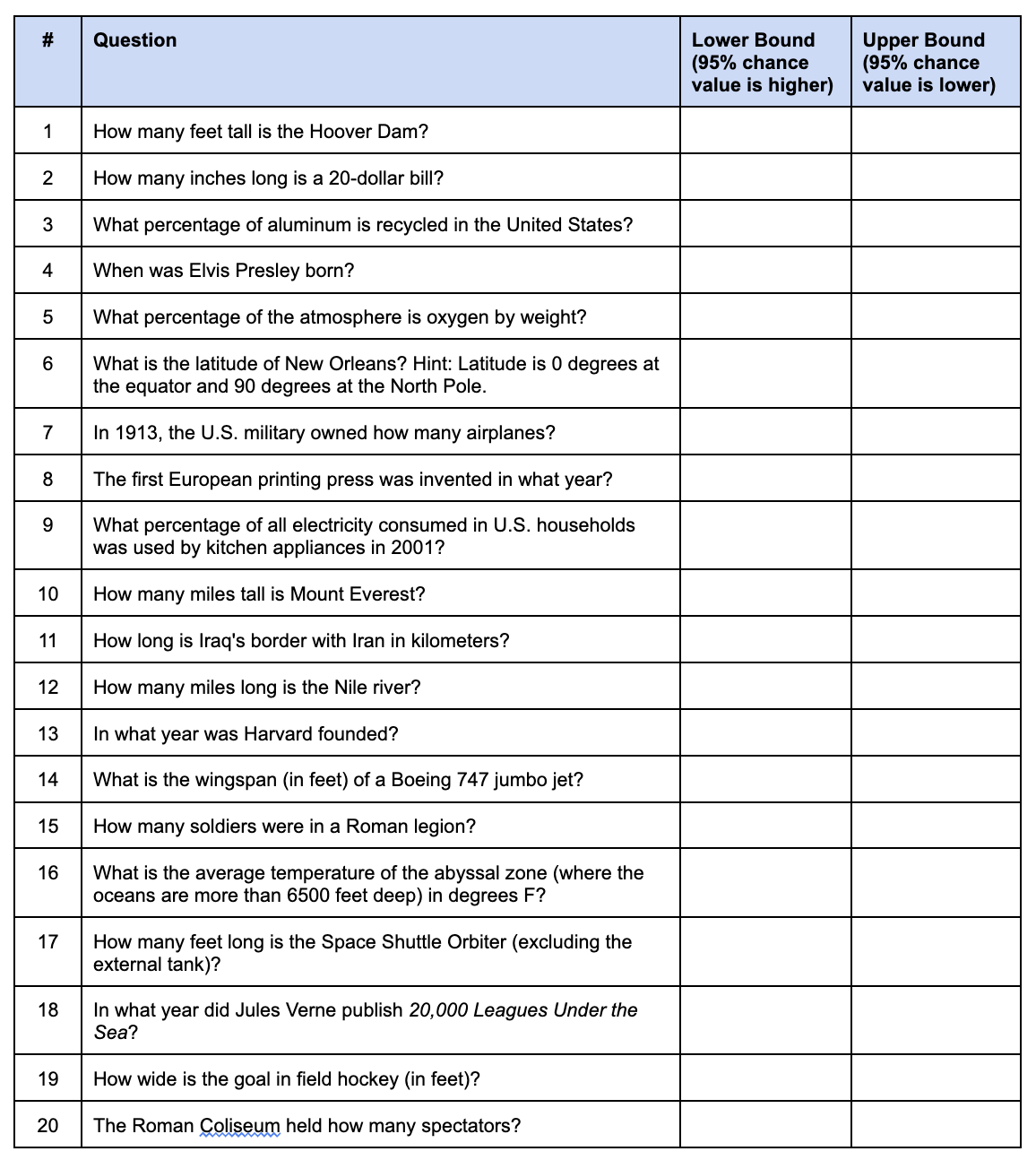
You can create you own version of this survey, with questions (1) having a similar degree of uncertainty across the general population, and (2) tailored for your audience's knowledge base.

Hubbard encourages the facilitator to offer a couple tips to the participants:

• Focus on what you do know
• Find bounds that are absurd, and move inward

The participants answers - as estimates - are collected, and evaluated. If an estimator were perfectly “calibrated”, then 90% (18 of 20) of their 90% CI ranges would contain the right answer to the question. A perfectly calibrated estimator would always get 18 of 20 answers to land “in their range”.

What Hubbard has found, in many years of conducting this exercise, is that participants average only around 11 of 20 successful 90% CI estimates. That is, they are overly confident in their ability to set the bounds around the answer.

In some participants, the opposite is true: underconfident estimators set “too-wide” ranges, and end up catching the actual answer more than 90% of the time.

Either way, the estimators could benefit from improving their “calibration”. But how?

Hubbard offers several techniques that can be taught and practiced, to improve results.

‍

Equivalent Bet Test - To reinforce the idea that the 90% CI range should aim to cover the value exactly 90% of the time, think of it like a gambler would. Imagine you have two options, and you’re asked to choose one, like a bet:

• Option A: You win $1000 if the true answer turns out to be between your upper and lower 90% CI bounds. If not, you win nothing.
• Option B: Spin a wheel with 10 equally sized slices, where one of the ten is labeled “Loser”, and the other nine are labeled “Winner”. If your spin lands on “Winner” you get $1000. If it lands on “Loser”, you win nothing.

‍

‍

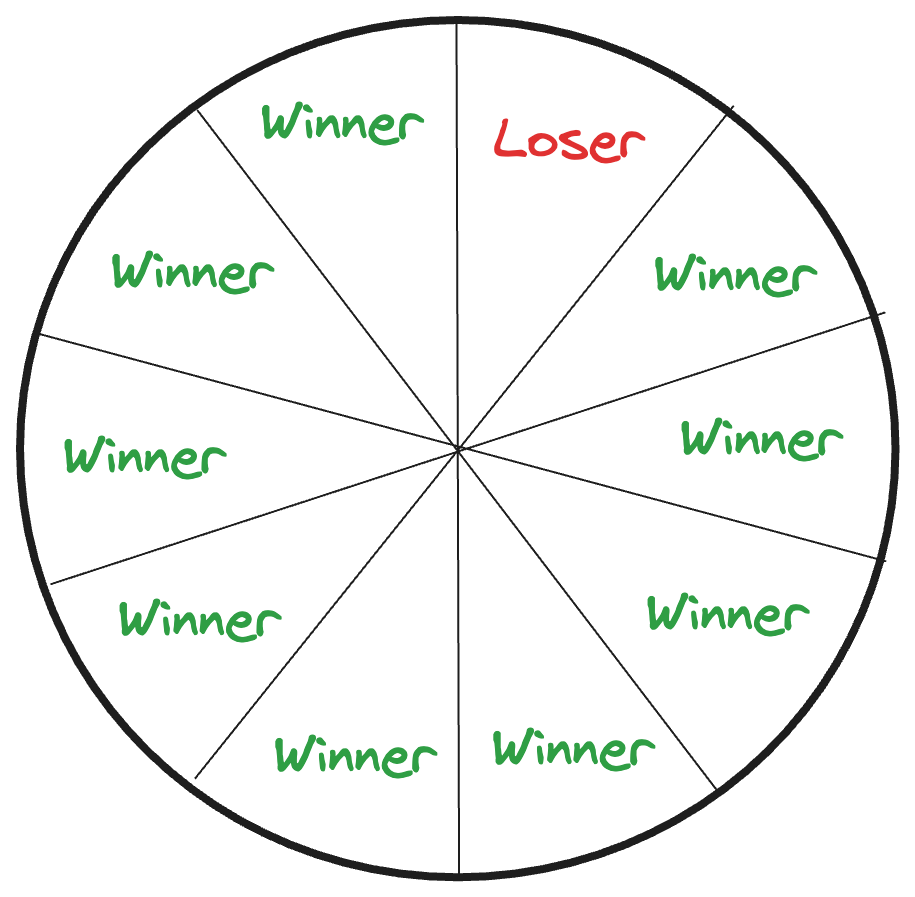
Which option do you prefer? Ha! Trick question! You should be indifferent.

• If you prefer Option A - your interval is too broad, consider reducing the range
• If you prefer Option B - your interval is too narrow, consider expanding the range

This mental trick helps estimators land on a range that truly has a 90% chance  (but no more) of including the value.

‍

‍Consider Potential Problems - Like a Pre-Mortem, this technique asks the estimator to assume that their estimate (as it currently stands) is wrong. Why might it be wrong? Provide possible explanations for both the upper bound, and for the lower bound. This thought experiment alone is usually enough to drive revisions in the placement of the bounds. 

Hubbard says it’s a way to fight our natural stubborn instincts: “We have to make a deliberate effort to challenge what could be wrong with our own estimates.”

‍

‍Avoid Anchoring - In this technique, look at each bound as a separate, independent question:some text

• For upper bound: At what point would there be only a 5% chance that the value is greater? (or, at what value are you “95% sure it’s going to fall above it…”)
• For lower bound: At what point would there be only a 5% chance that the value is lower? (or, at what value are you “95% sure it’s going to fall below it…”)

This approach avoids the problem of anchoring around a single estimate. When you initially think of the “correct” answer, you anchor there, and it’s harder to widen the range, and harder to arrive at ranges that aren’t symmetric around the anchor.

‍

‍Absurdity Test - This technique is another one designed to counter the anchoring effect, by reversing the thought process. Start with an absurdly wide range, then work to reduce the breadth, by eliminating values you know to be extremely unlikely. It reframes the question from “What do I think this value could be?” to “What values do I know to be ridiculous?”. This approach works well in situations where the estimator feels overwhelmed by the uncertainty (i.e. “I don’t know anything about this! How could I possibly provide an estimate?”).

‍

Like any training regimen, improvement results from repetition and feedback. First, estimators will learn of their inherent biases (e.g. over- or under-confidence). Second, they can practice the techniques to create better 90% confidence intervals. After completing a few rounds on these practice questions, they should be able to apply their newly calibrated estimation “instrument” to questions with uncertainty in their domain and context, with improved results.

Hubbard has been able to show - statistically - the improvement in capability in his cohorts of estimators over the years. He also points to a corollary benefit of the activity: “Calibration seems to eliminate many objections to probabilistic analysis in decision making.” So, when estimators better understand how to handle uncertainty in their own estimates, they are more open to thinking probabilistically about the world around them.

Hubbard says, “Apparently, the hands-on experience of being forced to assign probabilities, and then seeing that this was a measurable skill in which they could see real improvements, addresses those objections.”

So consider this exercise as a low-stakes way to start acknowledging uncertainty in your ways of working.

‍